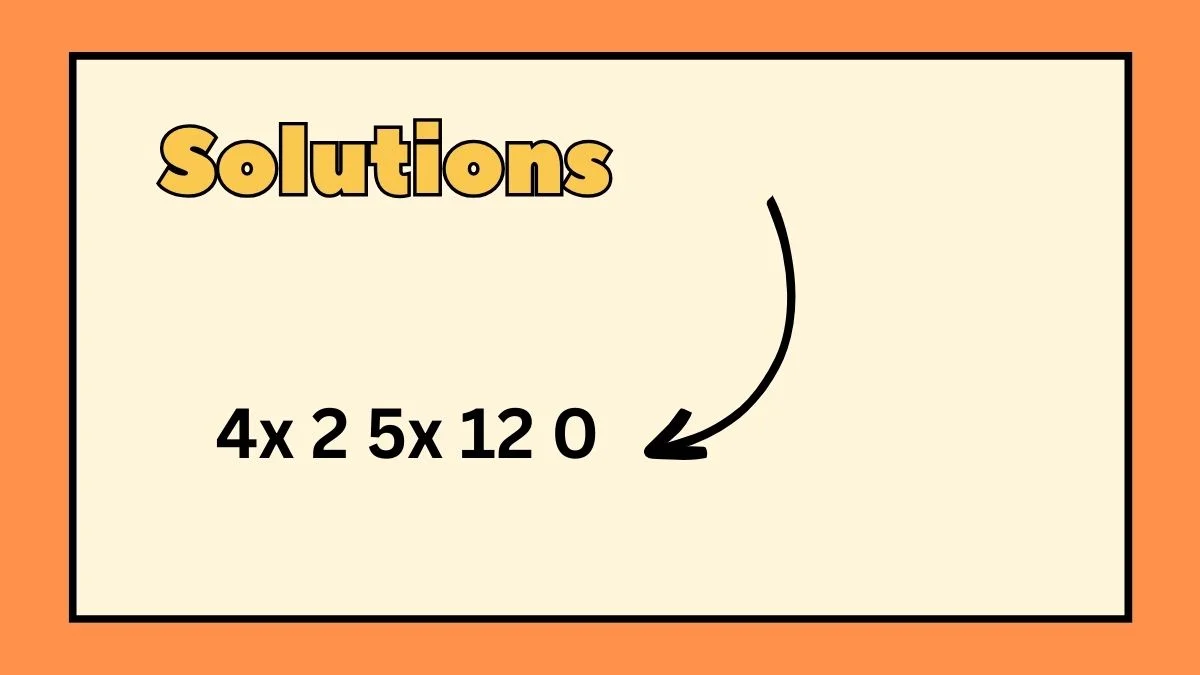
In the world of mathematics, equations often serve as powerful tools for understanding relationships between variables. The expression 4x 2 5x 12 0 is a quadratic equation, and in this article, we’ll delve into the process of solving it, exploring the solutions and implications of the mathematical expression.
Understanding the Quadratic Equation
The given expression represents a quadratic equation in the form ax^2 + bx + c = 0, where in this case, a = 4, b = -5, and c = -12. Quadratic equations are essential in various fields, including physics, engineering, and finance, as they model relationships with quadratic functions.
Solving the Quadratic Equation
The solutions of the quadratic equation can be found using the quadratic formula: �=−�±�2−4��2�x=2a−b±b2−4ac. Applying this formula to our equation yields two potential solutions for x.

Calculating the Solutions
To find the numerical values of �1x1 and �2x2, we must evaluate the expressions under the square roots and simplify the fractions. The discriminant (�2−4��b2−4ac) will determine the nature of the solutions.
Interpreting the Results
- If the discriminant is positive, there are two distinct real solutions for x.
- If the discriminant is zero, there is one real solution (a repeated root).
- If the discriminant is negative, there are two complex conjugate solutions.
Applications and Relevance
Quadratic equations find applications in various real-world scenarios. From predicting projectile motion to optimizing financial models, the ability to solve quadratic equations is crucial. By understanding the roots of the equation, one gains insights into the behavior of the associated quadratic function.
Conclusion
In conclusion, the expression 4x 2 5x 12 0 is more than just a collection of numbers and variables; it represents a quadratic equation with solutions that have real-world implications. Solving such equations not only enhances mathematical skills but also provides a valuable tool for addressing problems in diverse fields. As we navigate the complexities of mathematical expressions, we unveil the beauty of equations and their applications in understanding the world around us.
ALSO READ: Zearn Math: Transforming Education Through Engaging Online Learning